roadkills <- read.table("RoadKills.txt", header=T)
plot(roadkills$D.PARK, roadkills$TOT.N, xlab="Distance du parc", ylab="Nombre de morts")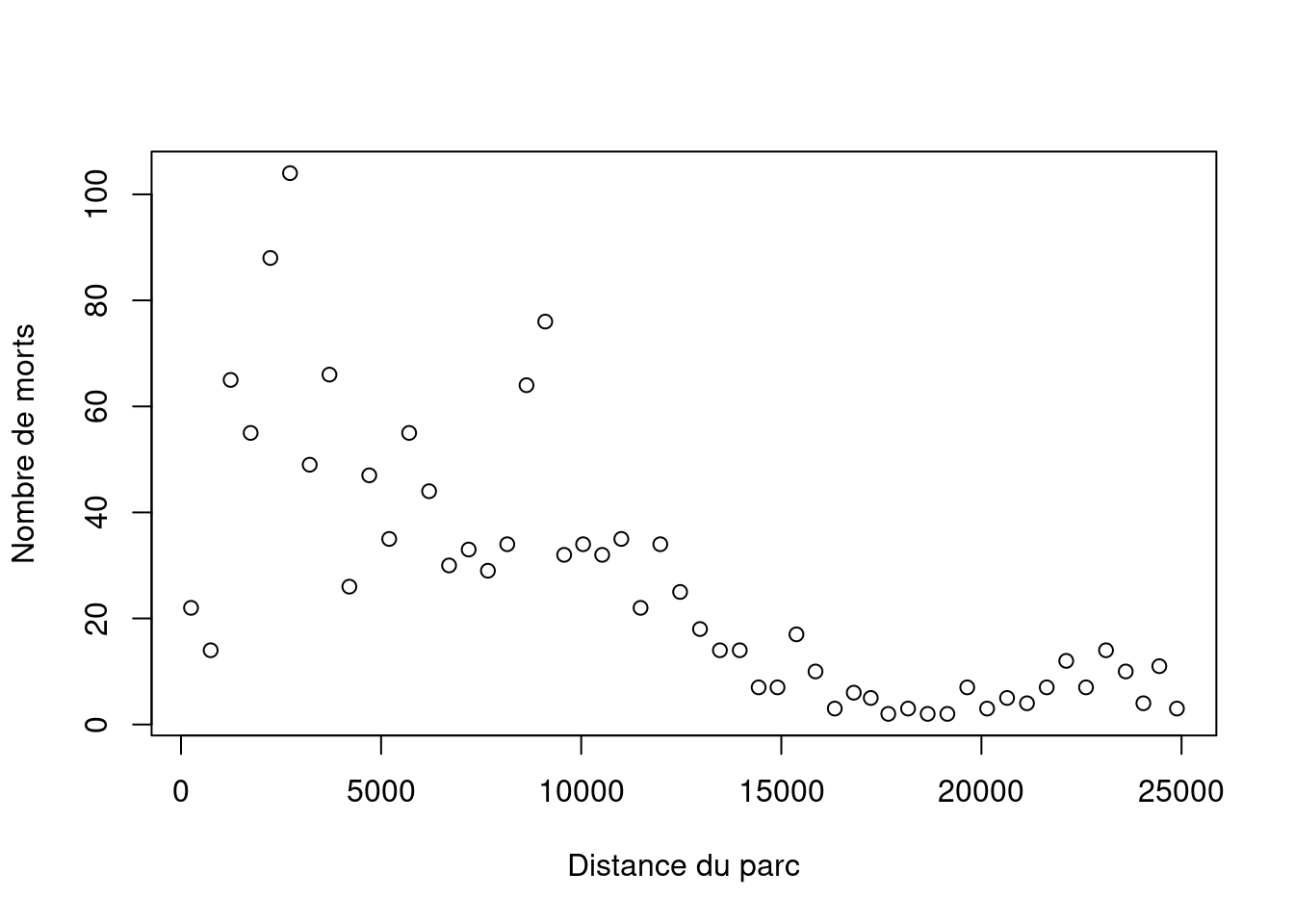
7 Modèles linéaire et additifs généralisés pour les données de comptage
7.1 Introduction
Un modèle linéaire généralisé (GLM) ou un modèle additif généralisé (GAM) se compose de trois étapes: (i) la distribution de la variable réponse, (ii) la spécification de la composante systématique en termes de variables explicatives, et (iii) le lien entre la moyenne de la variable réponse et la partie systématique.
Dans ce chapitre, nous nous concentrons sur les données de comptage et utilisons les distributions de Poisson et binomiale négative.
Un GLM se compose de trois étapes :
1. Une hypothèse sur la distribution de la variable réponse \(Y_i\) . Cette hypothèse définit également la moyenne et la variance de \(Y_i\) .
2. Spécification de la partie systématique. Il s’agit d’une fonction des variables explicatives.
3. La relation entre la valeur moyenne de \(Y_i\) et la partie systématique. On l’appelle aussi le lien entre la moyenne et la partie systématique.
7.2 Un GLM du jeu de données roadkills
Les données sont des comptages, et il semble y avoir une relation non linéaire, peut-être exponentielle, entre les victimes de la route et le D.PARK.
Notez également que la variation est plus importante pour des valeurs plus élevées de roadkills. L’ensemble de ces éléments nous donne tous les ingrédients d’un GLM de Poisson. Commencer avec seulement D.PARK comme variable explicative, et ignorer les 10 autres variables explicatives, est un choix pédagogique pour présenter le GLM de Poisson dans un manuel et n’est pas une recommandation générale pour l’analyse de ces données. Le GLM de Poisson suivant a été appliqué.